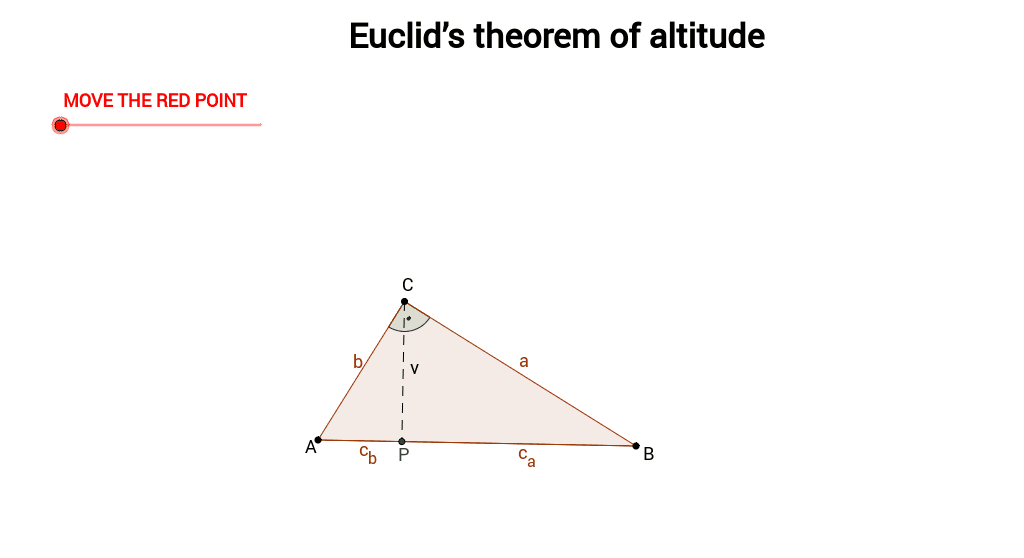
Euclid’s Theorem for class 10 exemplar is a very important theorem in geometry. It states that, given a line and any point not on the line, there is exactly one perpendicular distance from that point to the line. This allows for two quantities to be calculated: the length of a side of the triangle and the area of an equilateral triangle. The theorem can easily be extended to polygons with more than three sides by using parallel lines instead of a single straight edge. In fact, it is known as “the greatest common measurer” because it can also serve as a common divisor for all triangles and quadrilaterals in Euclid’s system (or other similar systems).

Euclid’s Theorem is named after the Greek mathematician Euclid, who is best known for his work on geometry. Although some aspects of Euclid’s theorem existed as early as 4000 BC (it was probably first discovered in Egypt), the majority of it was developed and proven by Euclid during his lifetime (325 before Jesus Christ to 265 after). He first introduced this theorem in Book I, Proposition 47 of “The Elements”, his most famous work. This book contains 13 volumes and, together with its companions, covers a wide range of subjects including straight lines, angles, circles, numbers, and proportions. Infinity Learn can provide the best study guide for class 10 Ncert exemplar solutions. 

How to calculate?

Euclid’s theorem gives a simple and useful way to calculate the side of a triangle and the area of an equilateral triangle. It is also easy to prove by constructing a diagram, but it requires some manipulation in order to do so. As such, it is sometimes called the “constructive proof”. An algebraic formula can be used in place of geometric construction, but this requires small changes to Euclid’s proof.

The theorem is widely used in higher mathematics, including geometry, algebra, trigonometry, and calculus. Other examples include:

The theorem is also used in particle physics. In general, the theorem states that if “P” and “Q” are points not on a line and if “A” is the altitude of “P” from the point “S”, then there is exactly one perpendicular distance from the point “S” to the line from “P” to “Q”. This distance can be easily calculated by applying Euclid’s algorithm. For particles at rest, it is a dimensionless quantity known as a Fermi length.

Euclid’s theorem can be applied to prove other results: for example, it can be used to prove that triangle inequality.

Euclid’s theorem can be used to prove theorems about triangles, quadrilaterals, and similar shapes. It can also be used to prove the properties of rectangles:

The proof that Euclid’s theorem is true is quite simple. By construction of a diagram, we can see that there is exactly one perpendicular distance from a point on the line to any side of a triangle. This distance can be calculated by applying a formula for the sum of the lengths of two sides (half the square on one side times half the square on the other side). The result is the distance of a triangle from one side to the midpoint of aside. Conversely, the formula for this distance can be used to find the gradient for an edge of a triangle.

Euclid constructed his proof in Book I, Proposition 47 of his “Elements”, written around 300 BCE. The first line states:

The proof proceeds by applying axiom 3) that “if equals are added to equals, then equals remain equal”. (This is equivalent to the fact that, if equals are subtracted from equals, then the result is a difference of equals; see decimal representation.)

Conclusion:

At first glance, this seems to be an application of Euclid’s axiom 1), which says that “a segment can be extended indefinitely”. However, this does not actually prove theorem 47. That is because Euclid’s axiom 1) has been picked out in such a way as to make it impossible for any segment to be extended indefinitely. It is better to read it as “If unequal magnitudes are added to unequal magnitudes, then unequal results will be obtained”.